[学校は人的資本を形成するのか? (1)教育の経済学] 
学校は人的資本を形成するのか? 〜分布区分とコーホート分析〜 [実証:日本のみ]を簡潔に説明します。
このページでは教育に対する経済学の理論を紹介し、数値例などで学歴間賃金格差の測り方の問題点を示します。
この問題点が実際の賃金データに与える影響に関しては、次ページの(2)賃金格差の実証分析を読んでください。
If you prefer English, go to (1)Economics of Education and (2)Wage Differentials in Japan.
10分で分かる『学校は人的資本を形成するのか?』:このページの日本語印刷版に当たる6ページの要約(PDF:約130KB)です。
Learn fallacy of wage differentials with cohort data in 10 minutes:このページの英語印刷版に当たる6ページの要約(PDF:約140KB)です。
平均間倍率の簡易シミュレーション:分布と人的資本形成効果を設定して、平均間倍率(賃金倍率)の推移を見ることができるExcelシミュレーション(約50KB)です。
Excelにおける回帰分析の目次:Excelでの回帰分析の手順を中心に、推定や統計量の説明が書いてあるHTMLです。
1. 高等教育に関する経済理論
大学などの高等教育は良くも悪くも、就職や賃金に結びついています。近代経済学では、就職や賃金に関わる高等教育のとらえ方として、人的資本論とシグナリング理論の二つの理論があります。それぞれの理論における進学・高等教育の意味は、以下の表のようになっています。
| 理論 | 進学・高等教育の意味 |
| 人的資本論 | 教育機関で学ぶことで知識や技能を身につけ、生産性⇒賃金が上がる。 |
| シグナリング理論 | 良い教育機関に入学・卒業することが頭の良さ、真面目さ、努力家の証明になる。 (生産性⇒賃金の上昇は不要で、もともと優秀な人を選別する。) |
仮に学歴別の賃金データがあったとしても、人的資本論とシグナリング理論の「どちらが現実的か?」という判別は困難です。また二つの側面が併存し、両方とも現実的である可能性があります。このため、「どちらが現実的か?」という論争は継続中ながらも決め手に欠いていました。しかし、このWebページと(2)賃金格差の実証分析を読むと、日本においてどちらの理論が現実的かが分かります。
- human capital theoryの訳語として人的資本論と呼ばれることもあれば、人的資本理論と呼ばれることもあります。物的資本と同様に経済成長の源泉と考えられたことから、マクロ経済学の経済成長論でこの名前がつきました。
- signaling theoryでシグナリング理論と訳す場合もあり、signaling hypothesisでシグナリング仮説と訳すこともあります。求職者(学生)が自分の能力を示すという意味でシグナリング(⇒シグナル:信号の発信)ですが、企業側の立場に立ってスクリーニング(審査、選別)という語句が使われる場合もあります。
- 人的資本論の権威のBecker(ベッカー)教授は1992年に、シグナリング理論の権威のSpence(スペンス)教授は2001年にアルフレッド・ノーベル記念経済学スウェーデン銀行賞を受賞しました。
2.1 学歴間賃金格差を測る賃金倍率
人的資本論とシグナリング理論のどちらが現実的かの議論をいったん離れ、学歴間賃金格差に焦点を当てます。賃金格差は政治、メディア、学会でもよく採りあげられます。また、学歴間賃金格差という場合は、主に大卒平均・高卒平均間の賃金格差を指しています。引き算の
![]()
を格差の指標とすると、物価の変化から影響を受けてしまいます。物価変化の影響のない割り算の

を格差の指標とするのが政府資料を中心に一般的になっています。この指標は「20%多い」や「1.2倍」と言える倍率での格差、つまりは賃金倍率です。 賃金倍率は解釈がしやすく、たびたび用いられますが、格差の指標として不適当であるというのが『学校は人的資本を形成するのか?』のスタート地点です。
- 賃金倍率はConcise Encyclopedia of Economics: Human CapitalやCurrent Population Reports: July 2002のように時系列で推移を見ることもあれば、OECD Science, Technology and Industry Scoreboard 2007のように国際比較に利用することもあります。
- 平成18年版の労働経済白書の分析のように、大卒平均賃金を分母にとって学歴間賃金格差の指標とすることもあります。この指標は、上記の賃金倍率の逆数となるので、縮小と拡大の変化は入れ換わります。それ以外に関しては、このWebページで示す論点は変わりません。
- パートタイム労働者、アルバイト、農林水産業、自営業、会社役員などを含めて、所得格差を議論する場合もあります。フルタイムの労働を行い、賃金(給与)として所得を得ているサラリーマンに関しては信頼できるデータを得やすく、(2)賃金格差の実証分析に対応させるために『賃金』という用語を使っています。学歴間の所得格差に関しても、学歴間の賃金格差と同じ測り方の問題があります。このWebページの『賃金』の部分を全て『所得』と読み替えても論点は変わりません。
- 労働経済学の学術論文では、上記の賃金倍率に対数をとって分析することがあります。対数変換は値の大小関係が変わらない単調変換ですので、このWebページで示す論点は変わりません。
2.2 賃金倍率の問題点
賃金倍率の問題点を簡単な数値例を用いて示します。世の中には生産性の高い順にAさん、Bさん、Cさんの3人が生まれてくるとします。Cさんを1として、Bさんは2倍、Aさんは3倍の生産性があり、生産性に見合う賃金をもらうことができるとします。生産性の高い順に大学に進学し、大学に進学したとしても生産性(⇒賃金)は変わらない場合を考えます。
- 家庭教育や初等教育で身につけた後天的な生産性と考えることもできます。
昔は、高卒以下の学歴で就職する人が大半で、Aさんだけが大学に進学していました。この時はAさんの賃金は3万円、Bさんの賃金は2万円、Cさんの賃金は1万円でした。時代の経過とともに進学する割合が増え、現代ではBさんも大学に進学するようになりました。物価も昔に比べて2倍になり、Aさんの賃金は6万円、Bさんの賃金は4万円、Cさんの賃金は2万円になりました。ここで、昔と現代で賃金倍率がどのようになるのかを見てみます。
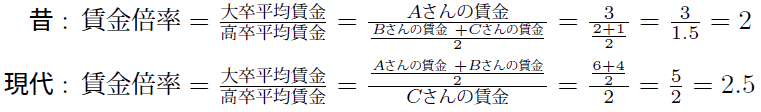
昔は2だった賃金倍率が、現代では2.5に上がります。昔も現代も大学の賃金に与える効果はゼロのままでAさん、Bさん、Cさんのもらっている賃金の比率は3:2:1で変わっていません。しかし、学歴間賃金格差の指標となっている賃金倍率は上昇してしまいます。
- 2.1 学歴間賃金格差を測る賃金倍率にあるように、物価が変化しても分子分母に同じ数をかけることになるので、賃金倍率への影響はありません。
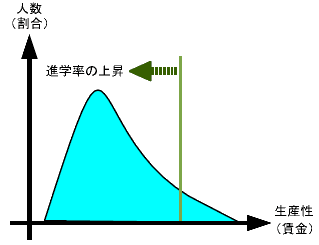 上の数値例では、生産性の高い人(Aさん)、普通の人(Bさん)、生産性の低い人(Cさん)が均等に一人ずつ存在する設定をしました。均等に存在する設定では、進学率の上昇は必ず賃金倍率の上昇をもたらします。一方で現実の生産性や賃金は、Bさんに相当する普通の人の割合が高くなっており、分布を書くと山の形になっています。また、とても高い賃金を得ている人が少数いるので、賃金分布は右裾が伸びた右図のようになっています。
上の数値例では、生産性の高い人(Aさん)、普通の人(Bさん)、生産性の低い人(Cさん)が均等に一人ずつ存在する設定をしました。均等に存在する設定では、進学率の上昇は必ず賃金倍率の上昇をもたらします。一方で現実の生産性や賃金は、Bさんに相当する普通の人の割合が高くなっており、分布を書くと山の形になっています。また、とても高い賃金を得ている人が少数いるので、賃金分布は右裾が伸びた右図のようになっています。
生産性や賃金に山形の分布を想定した場合、賃金倍率は進学率の上昇によって、いったん縮小した後に拡大します。手計算でも検算ができる数値例が下の表です。黄色いマスは全賃金倍率の中で一番小さい値を示しています。この設定においては10%の進学率では2.143であった賃金倍率が20%の進学率になると2.118に縮小し、さらに進学率が上がると反転して拡大します。
- 物価の影響を割り引いた実質賃金の引き算を格差の指標に用いることもあります。下の表が示すように、実質賃金の引き算も進学率の上昇によって変化します。
これまでは、単純化のために大学が生産性(⇒賃金)に与える効果をゼロとしていました。仮に±数十%の効果がある設定にしても、変化の形状は効果ゼロとあまり変わりません。いろんな分布や大学の効果における賃金倍率の変化は、Excelの平均間倍率の簡易シミュレーションでチェックすることができます。
また、これまでは必ず潜在的な賃金が高い順に進学をするという設定をしていました。そこでは進学する順、仕事の生産性、賃金を全く同じとして扱ってきました。現実には、勉強が苦手でも仕事の生産性が高い人もいますし、逆の場合もあります。また同じ生産性の人でも、働き方や運によって賃金が違うこともあります。進学する順番と賃金は一対一に一致する関係ではなく、正の相関関係にあると考えるのが自然です。ただ、平均賃金に注目する限りにおいて、正の相関関係は一対一に一致する関係に単純化することができます。
左下の動画は、学力と賃金(生産性)の二次元の分布と学力側からの区分を示しています。学力側で二次元の分布を区切ってから賃金側から見ると、学歴別の賃金分布になります。右下の動画は、大卒などの上位の学歴割合が増えた場合の学歴別の賃金分布の変化を示しています。赤い実線が大卒の賃金分布、青い破線が高卒の賃金分布を表していると考えることができます。こうした二次元の分布を設定すると、学歴別の賃金分布は重なり合う現実的な結果をもたらします。一方で、こうした二次元の分布を設定しても、各学歴の平均賃金は一次元の分布で考えた場合と同じになっています。よって、進学と潜在的な賃金の順番が一致していなくても正の相関関係があれば、賃金倍率に関する結果は一致する場合と同じです。
2.3 賃金倍率の要点まとめ
このページの要点を列挙すると
となります。日本を含め多くの国では、高等教育への進学率が上昇しました。この場合、[1]により個々人の賃金が不変の場合を含め、賃金倍率は必ず変化します。このため、賃金倍率は格差計測には不適当な指標です。
日本の賃金データを使った実証分析の学校は人的資本を形成するのか? (2)賃金格差の実証分析に続きます。
