[Excelにおける回帰分析 (3)最小二乗法の性質] 
Excel(エクセル)における回帰分析の手順と出力の意味を説明します。
このページでは、Excel での表示と対応させながら回帰分析(最小二乗法)の性質を紹介します。
推定や統計量の理解にも役立ちます。
Excelにおける回帰分析(最小二乗法)用乱数データ:乱数を用いて、推定値の挙動を見ることのできるExcel(約100KB)です。
分散の不偏推定量:偏差平方和を(n-1)で割ると分散の不偏推定量になることが視覚的に確認できるExcel(約80KB)です。
中心極限定理と擬似正規乱数:一様分布の標本平均が正規分布に近づくことや統計における検定のアイディアが視覚的に確認できるExcel(約60KB)です。
学校は人的資本を形成するのか? (1)教育の経済学:分布やシミュレーションを使って、学歴と平均賃金の関係を説明するHTMLです。
学校は人的資本を形成するのか? (2)賃金格差の実証分析:日本の学歴間賃金格差の実証分析を説明するHTMLです。
目次 : (2)分析ツールでの回帰分析の手順からの続きです。
記号と表記
ここでは、この『Excelにおける回帰分析』で用いる記号と表記を説明します。まず、回帰分析の被説明変数は![]() で表します。合計
で表します。合計![]() 個の標本を用いて推定するとし、
個の標本を用いて推定するとし、![]() 個目の標本の被説明変数は
個目の標本の被説明変数は![]() と下添え字をつけて表記します。また、回帰分析の説明変数は
と下添え字をつけて表記します。また、回帰分析の説明変数は![]() で表します。ところで
で表します。ところで![]() という単回帰においても
という単回帰においても![]() として、切片にあたる
として、切片にあたる![]() には常に1の説明変数がついていると見なせます。全ての標本に対して1をとる切片用の説明変数を1種類目に数え、データで与える説明変数は2種類目から数えます。標本
には常に1の説明変数がついていると見なせます。全ての標本に対して1をとる切片用の説明変数を1種類目に数え、データで与える説明変数は2種類目から数えます。標本![]() の
の![]() 種類目の説明変数は
種類目の説明変数は![]() と下添え字を並べて表記します。
と下添え字を並べて表記します。
回帰分析(最小二乗法)から得られた推定係数は![]() で表します。切片の推定係数は
で表します。切片の推定係数は![]() とし、
とし、![]() 種類目の説明変数の推定係数を
種類目の説明変数の推定係数を![]() と表記します。また、推定係数と説明変数があれば、当てはめ値(
と表記します。また、推定係数と説明変数があれば、当てはめ値(![]() の予測値)を算出することができます。当てはめ値を
の予測値)を算出することができます。当てはめ値を![]() (
(![]() ハット)と表記すると、合計
ハット)と表記すると、合計![]() 種類の説明変数による標本
種類の説明変数による標本![]() に対する
に対する![]() は、以下の(1)式のように表すことができます。
は、以下の(1)式のように表すことができます。
| (1) |
なお(1)式で表される![]() が被説明変数
が被説明変数![]() に一致するケースはほとんどなく、両者の間には推定エラー
に一致するケースはほとんどなく、両者の間には推定エラー![]() が存在します。推定エラー
が存在します。推定エラー![]() は、標本
は、標本![]() に関して回帰分析で説明できない部分に相当します。逆に言えば、結果的に算出された推定エラー
に関して回帰分析で説明できない部分に相当します。逆に言えば、結果的に算出された推定エラー![]() を用いて、当てはめ値
を用いて、当てはめ値![]() を調整すると、(2)式のように被説明変数
を調整すると、(2)式のように被説明変数![]() になります。
になります。
| (2) |
- 回帰分析(最小二乗法)よって得られた推定エラーは
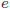 (イー)で表すのに対し、説明変数と被説明変数の間にある実際のノイズは
(イー)で表すのに対し、説明変数と被説明変数の間にある実際のノイズは (イプシロン)で表します。最小二乗法の問題点をふまえて高度な分析を行う場合には、
(イプシロン)で表します。最小二乗法の問題点をふまえて高度な分析を行う場合には、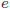 と
と をきちんと区別することが重要です。
をきちんと区別することが重要です。
3.1 説明変数と推定エラーの積の総和は0になる
回帰分析(最小二乗法)では、![]() 種類目の説明変数
種類目の説明変数![]() と推定エラー
と推定エラー![]() の積を
の積を![]() 個の標本で合計すると
個の標本で合計すると
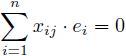 |
(3) |
と必ず0になります。0になっていることを確認したい場合は、乱数データの[乱数シート]でV〜Y列の62行目にある平均値がF9を押しても、0から動かないことで確かめてください。平均値が0なので、標本数![]() をかけた合計値も0になることが分かります。
をかけた合計値も0になることが分かります。
- 推定エラーの二乗和
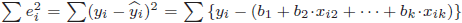 の最小化の必要条件は一階微分
の最小化の必要条件は一階微分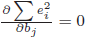 です。
です。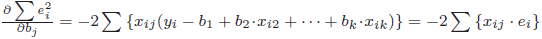 なので、一階微分=0は
なので、一階微分=0は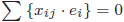 と書きかえられます。
と書きかえられます。
記号と表記に示したように、(1)式の切片である![]() には常に1の説明変数が付いていると考えることができます。すると(3)式の性質は、
には常に1の説明変数が付いていると考えることができます。すると(3)式の性質は、
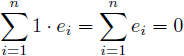 |
(4) |
と推定エラー![]() の総和が0と書きかえることができます。
の総和が0と書きかえることができます。![]() の平均を
の平均を![]() (
(![]() バー)とすると、切片を含めた回帰分析では、推定エラーの総和
バー)とすると、切片を含めた回帰分析では、推定エラーの総和![]() や平均
や平均![]() は必ず0になります。
は必ず0になります。
また、(2)式の両辺に![]() をかけ、総和をとると
をかけ、総和をとると
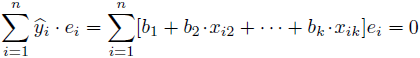 |
(5) |
と当てはめ値![]() と推定エラー
と推定エラー![]() の積の総和も0になることが分かります。総和が0なので、標本数
の積の総和も0になることが分かります。総和が0なので、標本数![]() で割った平均値も0になります。
で割った平均値も0になります。

3.2 回帰線は説明変数と被説明変数の標本平均を通る
(2)式の![]() を標本
を標本![]() で総和をとります。
で総和をとります。
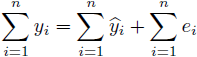 |
(6) |
また、(4)式で示されるように切片のある回帰分析では、(6)式の右辺第二項の![]() は0になります。よって(6)式は
は0になります。よって(6)式は
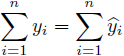 |
(7) |
と、被説明変数![]() と当てはめ値
と当てはめ値![]() の総和同士が等しい条件に書きかえることができます。総和が等しいので標本数
の総和同士が等しい条件に書きかえることができます。総和が等しいので標本数![]() で割った平均も等しくなります。よって
で割った平均も等しくなります。よって![]() の標本平均を
の標本平均を![]() (
(![]() バー)で表すと
バー)で表すと![]() です。また、当てはめ値の平均
です。また、当てはめ値の平均![]() を説明変数を用いて書くと
を説明変数を用いて書くと
| (8) |
となります。(8)式は[被説明変数![]() の平均]=[当てはめ値
の平均]=[当てはめ値![]() の平均]=[回帰式に説明変数
の平均]=[回帰式に説明変数![]() の平均を代入した値]であることを示しています。つまり、切片のある回帰分析において回帰線は必ず被説明変数
の平均を代入した値]であることを示しています。つまり、切片のある回帰分析において回帰線は必ず被説明変数![]() 、説明変数
、説明変数![]() の標本平均を通ります。このため、乱数データの[乱数シート]では、
の標本平均を通ります。このため、乱数データの[乱数シート]では、![]() の平均値〈B62〉と
の平均値〈B62〉と![]() の平均値での当てはめ値〈B67〉は常に一致します。
の平均値での当てはめ値〈B67〉は常に一致します。

ところで、切片を含めた回帰分析の特殊形の『切片のみでの回帰分析』を考えます。すると(8)式は
| (9) |
となります。つまり、切片のみの回帰分析において切片の高さ![]() は被説明変数の標本平均
は被説明変数の標本平均![]() になります。また、回帰分析(最小二乗法)の発想に戻ると(9)式は
になります。また、回帰分析(最小二乗法)の発想に戻ると(9)式は
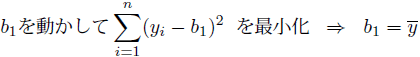 |
(10) |
となります。(10)式から切片のみの回帰分析において![]() を最小化する切片
を最小化する切片![]() は、被説明変数の標本平均
は、被説明変数の標本平均![]() であることが分かります。
であることが分かります。
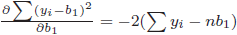 から、最小化の必要条件の一階微分=0は
から、最小化の必要条件の一階微分=0は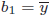 と書きかえられます。
と書きかえられます。
3.2 推定係数は平均的な効果になる
下図のような![]() の4つの標本に対して単回帰を行う場合を考えます。回帰分析から得られる
の4つの標本に対して単回帰を行う場合を考えます。回帰分析から得られる![]() の当てはめ値を
の当てはめ値を![]() 、
、![]() の当てはめ値を
の当てはめ値を![]() で表します。
で表します。
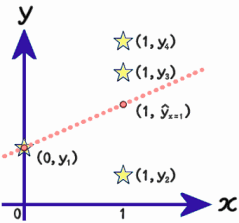
この例では![]() の標本は
の標本は![]() の1つしかありません。また、
の1つしかありません。また、![]() の値に依存せず、必ず
の値に依存せず、必ず![]() と
と![]() を結ぶ直線を書くことができます。このため、
を結ぶ直線を書くことができます。このため、![]() が
が![]() になることは明らかです。一方、
になることは明らかです。一方、![]() は(10)式の
は(10)式の![]() を
を![]() として、同種の問題を解くことになります。すると
として、同種の問題を解くことになります。すると![]() は
は![]() の標本における
の標本における![]() の平均値から、
の平均値から、![]() となることが分かります。
となることが分かります。
よって回帰線は![]() と
と![]() を結ぶ直線として
を結ぶ直線として
| (11) |
になります。(11)式では、![]() が1増えた場合の
が1増えた場合の![]() への効果は
への効果は![]() です。この推定係数は
です。この推定係数は![]() の平均値になっています。(11)式から類推されるように、回帰分析(最小二乗法)から得られる推定係数は、平均的な効果を算出しています。
の平均値になっています。(11)式から類推されるように、回帰分析(最小二乗法)から得られる推定係数は、平均的な効果を算出しています。
目次 : (4)回帰分析全体に関する出力に続きます。