[Excelにおける回帰分析 (4)回帰分析全体に関する出力] 
Excel(エクセル)における回帰分析の手順と出力の意味を説明します。
このページでは、回帰分析全体に関する出力を説明します。
Excelにおける回帰分析(最小二乗法)用乱数データ:乱数を用いて、推定値の挙動を見ることのできるExcel(約100KB)です。
分散の不偏推定量:偏差平方和を(n-1)で割ると分散の不偏推定量になることが視覚的に確認できるExcel(約80KB)です。
中心極限定理と擬似正規乱数:一様分布の標本平均が正規分布に近づくことや統計における検定のアイディアが視覚的に確認できるExcel(約60KB)です。
学校は人的資本を形成するのか? (1)教育の経済学:分布やシミュレーションを使って、学歴と平均賃金の関係を説明するHTMLです。
学校は人的資本を形成するのか? (2)賃金格差の実証分析:日本の学歴間賃金格差の実証分析を説明するHTMLです。
目次 : (3)最小二乗法の性質からの続きです。
このページでは、以下のように表示される回帰分析全体に関する出力を説明します。
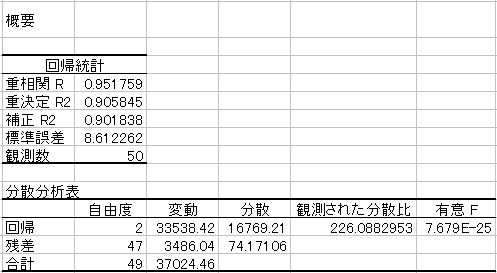
4.1 決定係数〈重決定R2〉:回帰分析の当てはまりの指標
回帰分析から得られた当てはめ値![]() が、どれだけ被説明変数
が、どれだけ被説明変数![]() を説明できているかを考えます。(2)式の
を説明できているかを考えます。(2)式の![]() の右辺第一項は『回帰分析によって説明できる部分』、右辺第二項は『説明できない推定エラーの部分』に相当します。第一項で説明できる部分が大きい方が、回帰分析の当てはまりが良いという印象があります。しかし、(2)式では平均的な
の右辺第一項は『回帰分析によって説明できる部分』、右辺第二項は『説明できない推定エラーの部分』に相当します。第一項で説明できる部分が大きい方が、回帰分析の当てはまりが良いという印象があります。しかし、(2)式では平均的な![]() の水準が高ければ、
の水準が高ければ、![]() が高くなります。そこで、(2)式の両辺から平均値を引いた偏差を用いて当てはまりの指標を作ります。
が高くなります。そこで、(2)式の両辺から平均値を引いた偏差を用いて当てはまりの指標を作ります。
また、偏差を用いても単純に総和をとって当てはまりの指標を作ることはできません。(4)式にあるように![]() の総和
の総和![]() や平均
や平均![]() は0になるからです。そこで、最小二乗法の発想のように二乗してから総和をとることを考えます。切片のある回帰分析では(7)式から
は0になるからです。そこで、最小二乗法の発想のように二乗してから総和をとることを考えます。切片のある回帰分析では(7)式から![]() 、(4)式から
、(4)式から![]() なので、(2)式の両辺から平均値
なので、(2)式の両辺から平均値![]() を引いた
を引いた![]() に対して二乗和をとります。
に対して二乗和をとります。
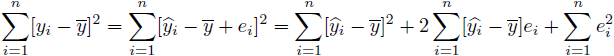 |
(12) |
(12)式の第二項の![]() は(4)式と(5)式より0になります。よって、(12)式は
は(4)式と(5)式より0になります。よって、(12)式は
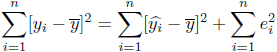 |
(13) |
と書けます。(13)式の形は[![]() の偏差平方和]=[
の偏差平方和]=[![]() の偏差平方和]+[
の偏差平方和]+[![]() の二乗和]です。 つまり、『被説明変数
の二乗和]です。 つまり、『被説明変数![]() の偏差平方和』は『説明できる分の
の偏差平方和』は『説明できる分の![]() の偏差平方和』と『説明できない分の
の偏差平方和』と『説明できない分の![]() の二乗和』に分解することができます。 (13)式の右辺第一項が第二項に比べて大きければ、回帰分析の当てはまりが良いことになります。割合の指標にするために(13)式の両辺を左辺で割ります。
の二乗和』に分解することができます。 (13)式の右辺第一項が第二項に比べて大きければ、回帰分析の当てはまりが良いことになります。割合の指標にするために(13)式の両辺を左辺で割ります。
 |
(14) |
(14)式の黄色に塗った部分が被説明変数![]() の偏差平方和に占める
の偏差平方和に占める![]() の偏差平方和で説明できる割合に相当し、決定係数と呼ばれます。 (14)式の右辺の二つの項は、分子分母ともに二乗の総和の形で必ずプラスです。その和が1になるので、決定係数は0から1の間の値になります。
決定係数〈重決定R2〉は回帰分析の当てはまりの指標であり、
の偏差平方和で説明できる割合に相当し、決定係数と呼ばれます。 (14)式の右辺の二つの項は、分子分母ともに二乗の総和の形で必ずプラスです。その和が1になるので、決定係数は0から1の間の値になります。
決定係数〈重決定R2〉は回帰分析の当てはまりの指標であり、![]() の偏差平方和のうち
の偏差平方和のうち![]() の偏差平方和によって説明できる割合を表します。
の偏差平方和によって説明できる割合を表します。
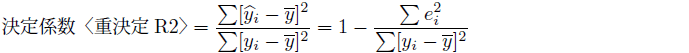 |
|
 |
(15) |
- 実証分析のレポートにおいて〈重決定 R2〉〈重相関 R〉〈補正 R2〉という用語は、ほとんど使われません。
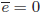 より、
より、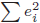 は
は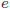 の偏差平方和とも言えます。また、推定エラーが残差と呼ばれることに対応して、
の偏差平方和とも言えます。また、推定エラーが残差と呼ばれることに対応して、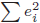 は残差平方和とも言われます。
は残差平方和とも言われます。
- 回帰分析の結果を示す際、決定係数は
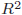 と表記されることがあります。
と表記されることがあります。
- 分散分析表の変動と書かれている列には、上から『
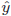 の偏差平方和』『
の偏差平方和』『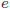 の二乗和』『
の二乗和』『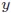 の偏差平方和』が表示されます。
の偏差平方和』が表示されます。
- 切片のみによる回帰では、(9)式より
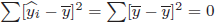 となるので、決定係数は0になります。
となるので、決定係数は0になります。
4.2 〈重相関R〉:決定係数の正の平方根
決定係数〈重決定R2〉は計算過程で二乗をとっているので、尺度を元に戻すために決定係数の正の平方根をとった値が〈重決定R2〉です。決定係数は0から1の範囲にあるので、正の平方根をとった〈重決定R2〉は必ず決定係数以上、1以下の値になります。
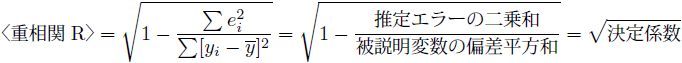 |
(16) |
- Excelでは『^』が累乗を表します。正の平方根は0.5乗なので、Excelのセルに『=数値^0.5』と入力して計算できます。また、Excelの関数の『=sqrt(数値)』を使うこともできます。
4.3 自由度修正決定係数〈補正R2〉:説明変数の数を考慮した当てはまりの指標
いったん行った回帰分析に説明変数を追加して、再び回帰分析をする場合を考えます。もし、追加した説明変数が全く回帰分析の役に立たない場合は、回帰分析の結果として追加した説明変数の推定係数は0になります。この場合、推定エラーの二乗和![]() も追加前の値と変わりません。一方で、追加した説明変数が少しでも回帰分析の役に立つ場合は、0以外の推定係数が得られます。この場合、
も追加前の値と変わりません。一方で、追加した説明変数が少しでも回帰分析の役に立つ場合は、0以外の推定係数が得られます。この場合、![]() は減少します。 実際には、無関係な説明変数であっても推定係数がちょうど0となることはありません。説明変数の追加によって、多少なりとも
は減少します。 実際には、無関係な説明変数であっても推定係数がちょうど0となることはありません。説明変数の追加によって、多少なりとも![]() は減少します。
は減少します。
(15)式で示したように、決定係数は説明変数の数に関係なく、![]() の
の![]() に占める割合から算出されます。このため、説明変数の追加は決定係数にプラスの影響しかありません。よって、無関係な説明変数であっても追加すればするほど、決定係数は増加します。
に占める割合から算出されます。このため、説明変数の追加は決定係数にプラスの影響しかありません。よって、無関係な説明変数であっても追加すればするほど、決定係数は増加します。
- 標本数と切片を含めた説明変数の数が等しければ、回帰分析が実行できる限り決定係数は必ず1になります。
そこで、説明変数を増やすことにマイナスの影響もある当てはまりの指標として、自由度修正決定係数を示すことがあります。 切片を含めて説明変数が![]() 種類あるとすると、自由度修正決定係数は以下の式で定義されます。
種類あるとすると、自由度修正決定係数は以下の式で定義されます。
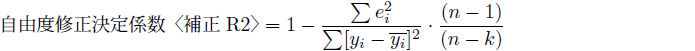 |
|
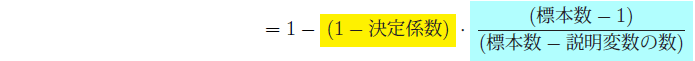 |
(17) |
自由度修正決定係数は、決定係数よりも小さく1以下の値となり、マイナスもあり得ます。説明変数を追加すれば決定係数を高め、(17)式の黄色に塗った値が減少します。一方で水色に塗った値は分母が減少することで増加します。説明変数を追加した場合、自由度修正決定係数の変化の方向は『黄色の減少分』と『水色の増加分』の逆方向の作用のどちらが大きいかの綱引きによって決まります。自由度修正決定係数〈補正R2〉は、説明変数の数を考慮した当てはまりの指標です。
- 自由度修正決定係数は、
 や
や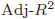 と表記されることがあります。
と表記されることがあります。
- 標本数
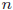 が説明変数
が説明変数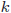 の数に比べてはるかに多い場合、(17)式の水色の部分が1に近くなります。この場合、自由度修正決定係数と決定係数の差は極めて小さくなります。
の数に比べてはるかに多い場合、(17)式の水色の部分が1に近くなります。この場合、自由度修正決定係数と決定係数の差は極めて小さくなります。
4.4 〔エラーの〕標準誤差:エラーの平均的なばらつきの推定値
(4)式に示されるように、切片のある回帰分析では、推定エラーの平均![]() は0です。しかし同じ平均0でも±1と±2のそれぞれ2つの標本では、±2の方がばらつきが大きいと言えます。このばらつきの指標を計算するために、まず
は0です。しかし同じ平均0でも±1と±2のそれぞれ2つの標本では、±2の方がばらつきが大きいと言えます。このばらつきの指標を計算するために、まず![]() と推定エラー
と推定エラー![]() を二乗をしてから総和をとります。その後で標本1つあたりの指標に変換します。
を二乗をしてから総和をとります。その後で標本1つあたりの指標に変換します。
単純に考えれば、![]() を標本数
を標本数![]() で割れば、標本1つあたりの指標になりそうです。しかし、
で割れば、標本1つあたりの指標になりそうです。しかし、![]() を標本数
を標本数![]() で割ると、真のばらつきに比べて小さめの推定値になる傾向があります。例えば、極端なケースとして標本が2つなら切片を含めた単回帰で完全に説明できて当たり前です。
この場合、
で割ると、真のばらつきに比べて小さめの推定値になる傾向があります。例えば、極端なケースとして標本が2つなら切片を含めた単回帰で完全に説明できて当たり前です。
この場合、![]() は0になります。しかし、エラーが0でばらつかないのではなく、切片を含めた説明変数の数と標本数が同じなので
は0になります。しかし、エラーが0でばらつかないのではなく、切片を含めた説明変数の数と標本数が同じなので![]() が0となっていると考えられます。標本数を
が0となっていると考えられます。標本数を![]() 、切片を含めた説明変数の数を
、切片を含めた説明変数の数を![]() とすると、説明できて当たり前でないのは
とすると、説明できて当たり前でないのは![]() の値に依存し、この値を自由度と呼びます。
の値に依存し、この値を自由度と呼びます。
- 回帰分析のみならず、一般的な不偏分散の推定も偏差平方和を標本数
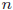 ではなく、
ではなく、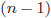 で割ります。分散の不偏推定量でF9を押せば、標本数で割ることのズレや不偏推定を視覚的に確認できます。
で割ります。分散の不偏推定量でF9を押せば、標本数で割ることのズレや不偏推定を視覚的に確認できます。
- 2つの点が散布図のどこにあったとしても、その2点を通る直線は必ず書けます。よって、標本が2つであれば、単回帰で完全に説明できます。
- (17)式は、水色の部分の分母が自由度になっていることから、自由度修正決定係数という名称になっています。
エラーの二乗和![]() を自由度
を自由度![]() で割ると、不偏分散と呼ばれる偏りのない標本1つあたりのエラーのばらつきが導出できます。また、不偏分散は計算過程で二乗をとっているので、正の平方根をとることで元の尺度の標準誤差という指標にします。
〔回帰統計の〕標準誤差は、エラーの平均的なばらつきの推定値です。
で割ると、不偏分散と呼ばれる偏りのない標本1つあたりのエラーのばらつきが導出できます。また、不偏分散は計算過程で二乗をとっているので、正の平方根をとることで元の尺度の標準誤差という指標にします。
〔回帰統計の〕標準誤差は、エラーの平均的なばらつきの推定値です。
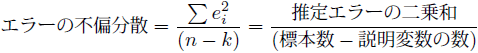 |
(18) |
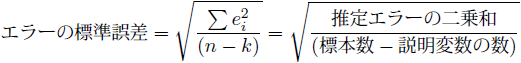 |
(19) |
- 分布から直接計算される分散の平方根を標準偏差(standard deviation)と言い、データから作られた統計量(例えば標本平均、残差平方和、推定値)の標準偏差を標準誤差(standard error)と言います。
- 分散分析表の[残差の行]と[分散の列]が交差するセルには、エラーの不偏分散が表示されます。
- エラーの不偏分散は
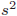 、エラーの標準誤差は
、エラーの標準誤差は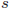 で表されることがあります。
で表されることがあります。
4.5 〈分散分析表〉と〈有意F〉:切片以外の説明変数は全て無効の検定と確率の上限
統計学や計量経済学では『異なっていない(同質)』や『効果がない(無効)』を主張する仮説を帰無仮説と言います。一方、帰無仮説の反対側の『異なっている(異質)』や『効果がある(有効)』を主張する仮説を対立仮説と言います。直接、対立仮説を肯定することが難しい場合、帰無仮説を否定することで間接的に対立仮説を肯定するという手続きをとります。
〈分散分析表〉は『切片以外の全ての説明変数は無効』⇒『切片以外の説明変数の真の係数は全て0である』という帰無仮説の検定を行っています。 この帰無仮説が正しい場合、切片だけで回帰分析をしても、説明変数を入れて回帰分析をしても、推定エラーの二乗和![]() に大きな差がないと考えるのが自然です。切片だけで回帰分析をした場合、(10)式から
に大きな差がないと考えるのが自然です。切片だけで回帰分析をした場合、(10)式から![]() となり、推定エラーの二乗和は
となり、推定エラーの二乗和は![]() と被説明変数
と被説明変数![]() の偏差平方和そのものになります。よって、切片以外の説明変数を追加することで減少した推定エラーの二乗和は
の偏差平方和そのものになります。よって、切片以外の説明変数を追加することで減少した推定エラーの二乗和は![]() となり、(13)式から
となり、(13)式から![]() であることが分かります。
であることが分かります。
- Excelには〈分散分析表〉と表示されますが、回帰分析のF検定を分散分析と呼ぶことは稀です。統計学で一般に分散分析と呼ばれるANOVA(analysis of variance)は、他の分析ツールとして存在します。同じF分布を使った検定ですが、回帰分析では『F検定』や『複数制約』と呼ぶのが一般的です。また、〈有意F〉という用語を使うことはなく『複数制約のP値』が一般的です。
〈分散分析表〉の[分散の列]には、左隣のセルの![]() を
を![]() で割ることで、『説明変数あたりの推定エラーの二乗和の減少』を表しています。その1つ下のセルには(18)式で算出される『説明変数を入れても残ったエラーのばらつき』の不偏分散が表示されます。〈観測された分散比〉は以下の(20)式の形で、この2つの数の比率をとっています。
で割ることで、『説明変数あたりの推定エラーの二乗和の減少』を表しています。その1つ下のセルには(18)式で算出される『説明変数を入れても残ったエラーのばらつき』の不偏分散が表示されます。〈観測された分散比〉は以下の(20)式の形で、この2つの数の比率をとっています。
 |
(20) |
また〈観測された分散比〉は、以下のように変形して決定係数で表すことができます。
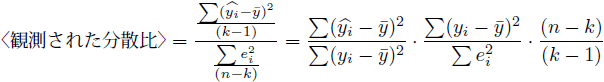 |
|
 |
(21) |
当てはまりの指標である決定係数が高ければ、(21)式の黄色に塗られている分数の分子が大きく、分母が小さいことで〈観測された分散比〉も高くなることが分かります。
(20)式から『説明変数あたりの推定エラーの二乗和の減少』が大きいほど、(21)式から『決定係数』が大きいほど、〈観測された分散比〉は大きくなることが分かります。このため、〈観測された分散比〉が大きい場合は『切片以外の説明変数の真の係数は全て0である』という帰無仮説は不自然になります。この不自然という感覚を統計で表したのが、〈分散分析表〉の〈有意F〉です。有意Fは『切片以外の全ての説明変数の効果が0である』という帰無仮説のもとで、偶然によって標本が観測されてしまう確率の上限を示しています。
- 有意FのFは、F分布を指しています。帰無仮説が正しければ〈観測された分散比〉は自由度
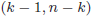 のF分布に従うことが知られています。
のF分布に従うことが知られています。
乱数データの[固定シート]〈P21〉表示されている〈有意F〉の[7.68E-25]は![]() を表し、ゼロが25個ならぶほど小さい数です。この場合、「『全ての変数が無効』という帰無仮説が正しければ、
を表し、ゼロが25個ならぶほど小さい数です。この場合、「『全ての変数が無効』という帰無仮説が正しければ、![]() 以下の確率でしか起こらないことが起こった。」⇒ 「帰無仮説は不自然で、ほぼ確実に効果のある説明変数がある。」という解釈になります。
以下の確率でしか起こらないことが起こった。」⇒ 「帰無仮説は不自然で、ほぼ確実に効果のある説明変数がある。」という解釈になります。
- Excel関数から直接F分布による統計量を計算することもできます。[=FDIST(観測された分散比,回帰自由度(k-1),残差自由度(n-k)]=[FDIST(226.0883,2,47)]と入力すると、[7.68E-25]が出力されます。
目次 : (5)説明変数に関する出力に続きます。